

Die meisten geheimen Botschaften der großen Pyramiden in Ägypten werden ja in ihren Dimensionen gesehen, aber auch schon ihre Platzierung auf der Erde soll ein Hinweis auf ihre Besonderheit sein. Auch die meisten diese Rätsel haben schon mehr als 100 Jahre auf dem Buckel. Aber wie wir schon auf den vorherigen Seiten gesehen haben: "Alt" bedeutet nicht unbedingt "korrekt". Schauen wir uns daher nun mal die von Däniken propagierten Standorträtsel an.
|
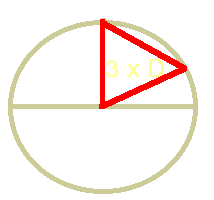
| Fig. 1 – Dreieck |
Rätsel (11) lautet: "Der Abstand der großen Pyramide vom Mittelpunkt der Erde ist genauso groß wie der Abstand zum Nordpol und entspricht somit dem Abstand vom Nordpol zum Erdmittelpunkt."
Dies ist mit Abstand das am meisten verbreitete „Rätsel“ der Großen Pyramide und wird in praktisch jedem Buch verwurstet, in dem es um die Rätsel der Pyramiden geht. Und eines der falschesten überhaupt, und das gleich in mehrfacher Hinsicht.
Das fängt schon damit an, dass die Formulierung schlicht falsch ist. Gemeint ist, dass die drei roten Linien in dem nebenstehenden Bild alle gleich lang sind. Die Strecke quer durch die Erde vom Mittelpunkt der Erde zu den Pyramiden, von den Pyramiden quer durch die Erde zum Nordpol, und zwangsläufig die Strecke vom Pol zurück zum Erdmittelpunkt. Für uns Erdenwürmer wäre aber die Strecke zum Pol die, die wir auf der Oberfläche zurücklegen würden.
„Gut“, wurde argumentiert, das sei doch erbsenzählerisch, der Autor habe doch zweifelsfrei dieses Streckendreieck gemeint. Und da stimmt's doch.
Leider nein, und das gleich in doppelter Hinsicht. Die Pyramide müsste auf einer idealen Kugel exakt auf 30° Nord stehen, damit dies erfüllt ist. Sie steht aber rund 2,5 Kilometer weiter südlich. Das ist zwar nicht viel, aber wir sollten in Erinnerung behalten, dass diese Pyramide ja angeblich ein Zeichen fremder Raumfahrer sein soll. Wir mit unserer Technik, die definitiv noch nicht zu interstellaren Reisen taugt, können aber schon Fehlpositionierungen im Zentimeterbereich feststellen. Noch besser: Sogar schon zu Napoleons Zeiten vor über 200 Jahren war die Messtechnik so weit, Abweichungen von weniger als 100 Metern zu erkennen.
Als Zeichen einer außerirdischen Planung ist dies glaube ich ziemlich ungeeignet.
Jaha, meinte ein englischer Pyramiden-Autor, ich mache da ja einen ganz dicken Fehler, da ich die Ellipsenform der Erde nicht berücksichtige. Täte ich das, würde alles wieder stimmen. Wirklich?
Es stimmt, der Dreieckssatz gilt nur für perfekte Kreise, die der Querschnitt einer perfekten Kugel sind. Die Erde ist aber keine perfekte Kugel, sondern ein Rotationsellipsoid. Aufgeschnitten ist die Schnittfläche eine Ellipse und kein Kreis. Der Poldurchmesser ist um etliche Dutzend Kilometer geringer als der Äquatordurchmesser.

|
| Fig. 2 - Ellipsoid |
Ein Kreis hat einen konstanten Radius. Eine Ellipse hat aber zwei Extremwerte bei der Ausdehnung: Die „große Halbachse“, die den maximalen Radius beschreibt (horizontale Linie im Bild), und die „kleine Halbachse“, mit der man den kleinsten Radius bezeichnet (vertikale Linie). Eine Ellipse mit der großen Halbache a als Radius eines Kreises und einer kleinen Halbachse b die kleiner ist als der Kreisradius, liegt also immer komplett innerhalb eines Kreises mit Radius a, wie im Bild zu erkennen ist.
Soweit einfach zu verstehen. Kommen wir nun zu den uns interessierenden Strecken. Auf einem Kreis liegt 30° Nord immer auf dem Äquidistanz-Punkt für Pol und Mittelpunkt, bei einer Ellipse aber nie. Um diesen Punkt auf einer Ellipse zu berechnen benötigen wir die Ellipsengleichungen der Mathematik, mit denen das Problem formal lösbar ist.
Für die folgenden Berechnungen benutze ich Grafiken und Formeln von dieser Internetseite (Longitude and Latitude Conversions), die die Herleitungen sehr gut erklären. Schauen wir uns zunächst diese Grafik an:
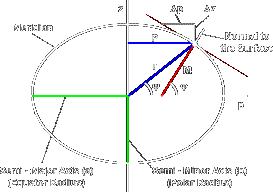
Aus ihr geht hervor, dass die geographische Breite Φ nicht identisch mit dem Positionswinkel Ψ ist, und zwar, weil die Breite über die Höhe des Himmelspols über dem Horizont eines Ortes definiert ist. Dieser Horizont steht aber bei einer Ellipse nicht senkrecht auf der Verbindungslinie zum Ellipsenmittelpunkt, wie man auf der Grafik sehen kann. Um mit mathematischen Formeln, die mit dem Positionswinel arbeiten, rechnen zu können, muss man daher die Koordinaten transformieren.
Was wir zur Bestimmung benötigen, ist einmal der echte Radius des Breitenkreises von Gizeh, im oberen Bild P genannt. Dann benötigen wir den vertikalen Abstand von Gizeh zum Äquator. Mit diesen beiden Werten können wir, zusammen mit dem Pol- und Äquatorhalbmesser der Erde, die beiden gewünschten Strecken r (Abstand zum Erdmitttelpunkt bei Gizeh und rp, den Polabstand, berechnen.
P erhält man aus der folgenden einfachen und einsichtigen Formel (aufgelöste Formel (10) auf der gelinkten Seite)
bei der a der Äquatorradius (große Halbachse) von 6378140 Metern ist, und b der Polradius von 6356775 Metern.
Die Höhe von Gizeh über dem Äquator kann man durch Auflösen der Ellipsengleichung
|
| Fig. 4 - Abstände |
nach z errechnen. Die Entfernung zum Erdmittelpunkt und zum Nordpol kann nun ganz einfach jeweils über den Satz von Pythagoras ermittelt werden. Der Abstand zum Mittelpunkt r ist einfach die Quadratwurzel von (P2+z2), der Abstand zum Pol rp ist die Quadratwurzel aus ((Polradius-z)2+P2), da beide Strecken die Hypotenuse eines rechtwinkligen Dreiecks sind.
Für 30° Nord (der Einfachheit halber; die Große Pyramide steht, Sie erinnern sich, 2,5 km südlich davon) ergeben sich folgende Werte:
| P | Z | r | rp | Differenz |
|---|---|---|---|---|
| 5528254 m | 3170392 m | 6372832 m | 6380802 m | 7969 m |
Die Linie zwischen 30° Nord und Pol ist also um schlappe 7,969 km länger als der Abstand zum Erdzentrum. Dies ist NICHT der Abstand zum echten Äquidistanz-Punkt, sondern nur der Unterschied in der Streckenlänge!
Der wahre Äquidistanz-Punkt liegt also etliche km weiter im Norden - und die Pyramiden liegen sogar noch 2,5 km weiter südlich von 30° Nord.
Um den Punkt zu finden, bei der beide Längen übereinstimmen, muss man "nur" ein P finden, bei dem die beiden Hypotenusen der beiden Dreiecke gleich lang sind. Die Herleitung erspare ich mir hier (ist ja keine Mathe-Seite), die gesuchte geographische Breite ist allerdings 30,0833°. Die Entfernung auf der Oberfläche kann man nun anhand der Länge eines Breitengrades auf der Höhe von 30° Nord berechnen. Die Webseite Length of 1 of Lat and Lon gibt darüber Auskunft: Die 0,0833 entsprechen 9234 Metern, der Punkt der Längengleichheit liegt daher knapp 12 km nördlich von Gizeh, ungefähr bei der Ortschaft Embaba am Beginn des Nildeltas.
Tja, wieder nix. Damit steht's dann 8:11 gegen die Pyramidenrätsel.
Der entsprechende Autor ließ sich dadurch aber nicht beeindrucken, da seine Pyramidengürtel-These eh' einen Punkt etwas nördlich von Gizeh als „idealen geplanten“ Pyramidenstandpunkt ermittelt habe (aber die Sternengötter waren wohl zu blöd, um auch dort zu bauen). Und ein anderer Autor, der die Grenze von Ober- und Unterägypten (und ebenfalls „geplanten“ Pyramidenstandort) bei 30,06° Nord angesetzt hatte, fand, dass 30,083° nicht sooooo weit entfernt davon liegt, und fand daher, dass das Ergebnis meiner Rechnung daher von einer beeindruckenden Kenntnis der alten Ägypter von der wahren Form der Erde zeuge. Und das Nildelta sei ohne jeden Zweifel künstlich angelegt, um diesen Punkt zu zelebrieren.
Erneut zeigt sich hier die Flexibilität der Grenzwissenschaft: Eine These wird widerlegt - sei's drum, man hat noch eine andere im Ärmel...
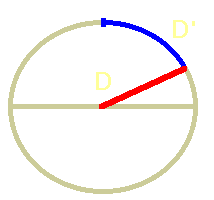
|
| Fig. 5 - Bogen |
Bevor noch jemand kommt, dass es vielleicht doch mit der Strecke an der Oberfläche klappen könnte, hier eine kleine Überschlagsrechnung auf einer perfekten Kugel.
Die echte Entfernung, also die Strecke D', die wir auf der Erdoberfläche zurücklegen müssen, ist, wie wir anhand der Skizze einwandfrei erkennen können, erheblich länger als die mathematische Sehne, die durch die Dreiecksseite gebildet wird. Gut 400 km, um genauer zu sein. 400 km länger als der Abstand zum Erdmittelpunkt. Um also wirklich gleiche Entfernungen darzustellen, müssten die Pyramiden dort stehen, wo diese Bogenlänge gleich dem Mittelpunktsabstand wäre. Also irgendwo nördlich von Kreta im Mittelmeer :-)
Bei dieser großen Differenz müssen wir uns auch nicht mit Ellipsengleichugen herumschlagen, die lediglich ein paar Kilometer Differenz ergeben würden.
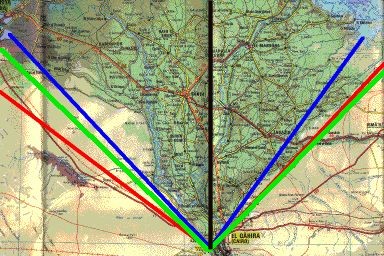
Rätsel (4) sagt: "Die Pyramiden-Winkel teilen die Deltaregion am Nil in zwei gleiche Hälften"
Das Delta ist der Mündungsbereich des Nils, eine fruchtbare, fächerförmigeRegion in der sich der Nil in Dutzende von Nebenarmen aufteilt. Aber welches Delta ist gemeint? Das heutige? Oder das Delta vor viereinhalb tausend Jahren? Dass die Behauptung mit dem heutigen Delta nicht stimmt, zeigt die Karte links: Die Westhälfte (alles links der senkrechten schwarzen Linie) umfasst zweifelsfrei weit mehr Fläche als die Osthälfte! (Die Pyramide steht am Schnittpunkt der Linien)
Wie das Nildelta vor 5000 Jahren genau aussah, ist heute unmöglich feststellbar, daher ist diese Aussage nur eines: vollkommen sinnlos, außer die Theosophen des 19. Jahrhunderts, die diese These um 1850 veröffentlichten, besaßen ene Zeitmaschine.
Eine andere, damit verwandte Behauptung ist, dass die Pyramidendiagonalen „das ganze Nildelta umschließen“ sollen. Zuerst sollte geklärt werden, was "umschließt das gesamte Delta" bedeutet. Man kann die maximale Winkelausdehnung so interpretieren, dass das gesamte durch das Delta bewässerte Land und die maximale Ausdehnung aller zum Delta gehörigen Wasserläufe eingeschlossen wird (rot), oder man betrachtet nur die östlichste und westlichste Mündung aller zum Delta gehörenden Wasserläufe ins Mittelmeer (blau).
Auf den ersten Blick ist zu sehen: Die Pyramide (Schnittpunkt der Linien) steht asymmetrisch zum Nildelta. Sie müsste rund 20 km weiter östlich im Mokkatam-Gebirge stehen, um die Auflage des „Scheitelpunkts“ zu erfüllen. Außerdem ist die weiteste Öffnung (die alle Wasserläufe des Deltas umschließt) weiter als 90°, während die zweite Delta-Definition einen geringeren Öffnungswinkel aufweist. Die Öffnung, die die Pyramide aufspannt (grün) ist im Osten weiter als das Delta, im Westen umfasst sie dagegen nicht den gesamten Bereich. Sie erfüllt daher keine der beiden Delta-Bedingungen, sondern liegt halt irgendwie so in der Mitte - und scheidet als supernatürliche Erklärung aus.
Ach ja: Dieselbe Bedingung erfüllen übrigens noch weitere Pyramiden, und sogar besser. Da der Nil südlich von Gizeh nach Osten fließt, schließen die Pyramiden von el-Aryan und Abusir das Delta weit besser ein als die geheimnisvolle große Pyramide :-)
Äußerst witzig: selbst auf dem Originalbild des Erfinders dieses Rätsels, Piazzi Smyth, haut es nicht hin. Man sieht sowohl im Osten wie im Westen Wasserarme, die aus dem markierten Bereich herauslaufen, und die dunklen Fruchtlandgrenzen liegen komplett außerhalb dieser Zone.
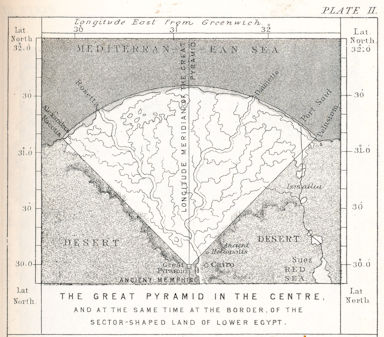
Neuer Punktestand: 7:12 gegen die Pyramidengeheimnisse.
Rätsel (2) sagt: Die Pyramide liegt im Zentrum der Festlandmassen der Erde. Aus der Erklärung geht leider nicht besonders deutlich hervor, was damit gemeint ist. Die Pyramidologische Urquelle Smyth sagt dazu:
"Der Meridian durch die große Pyramide ist die längst mögliche Nord/Süd-Strecke über Land, und der durch die Pyramide verlaufende Breitengrad ist die längst mögliche Ost/West-Verbindung über Land. Die Pyramide liegt daher im Massesnchwerpunkt aller Kontinente"
OK, das ist deutlicher. Und zeigt, dass auch EvD's Rätsel (3b) zu dieser Behauptung gehört:
Der Meridian der durch Gizeh läuft ... ist außerdem der am längsten über Land laufende Nord-Süd-Meridian und bildet den natürlichen Nullpunkt für die Längenmessung des ganzen Erdballs
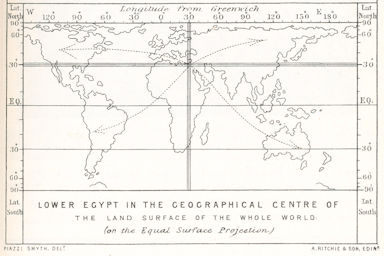
Bildlich sieht die Behauptung aus wie die Zeichnung oben. Die beiden eingezeichneten Linien sollen nach Smyth und Däniken die jeweils längsten Landlinien darstellen. Dummerweise stimmt auch diese Behauptung nicht, wie jeder anhand eines Globus selbst nachprüfen kann. Der längst mögliche Meridian (also Nord-Süd-Halbkreis von Pol zu Pol) findet sich gute 250 Kilometer westlich der großen Pyramide. Er verläuft, wie Sie selbst nachmessen können, fast 2000 Kilometer weiter über Land als der durch die große Pyramide! Woher diese Fehleinschätzung? Ganz einfach, das Rätsel stammt aus der Mitte des 19. Jahrhunderts - und zu der Zeit kannte man den Kontinent Antarctica noch nicht! 1821 Wurde erstmals Land entdeckt, das zu Antarctika gehörte, und in den folgenden Jahren betraten verschiedene Walfänger und Entdecker unterschiedliche Regionen von Antarctica, aber ob das ein Kontinent war, oder nur verstreute Inselchen war schlicht unbekannt Das kann man ja auch auf der Skizze von Smyth erkennen. Rechts und links unten erkennt man vage Andeutungen der Antarktis, aber das war es denn auch.
Heute aber kennen wir Form und Größe dieser Landmasse, und beziehen wir sie mit ein, löst sich dieses "Rätsel" in Luft auf.
|
| Fig. 8 - Realität |
Auch der Breitengrad durch die Pyramide verblasst gegenüber den Strecken, die den größten Teil von Asien mitnehmen. Nach meinen Messungen dürfte 50 Grad Nord der beste Kandidat für den längsten Land-Breitengrad abgeben, er verläuft mit rund 16000 Kilometern ebenfalls rund 2000 Kilometer länger über Land als 30 Grad Nord. Das "wahre" Zentrum der Erde läge daher ein paar Kilometer westlich von Kiew in der Ukraine! Auch dies ist mit ein wenig Geduld selbst überprüfbar! Was ist hier die Fehlerursache? Ganz einfach, Smyth berücksichtigte Kartenverzerrungen nicht mit! Freundlicherweise vermerkt er das aber auch auf seiner Skizze: "On the equal surface projection" steht da. Sein Geheimnis gilt also nicht für die Erde, sondern nur für eine ganz bestimmte Kartenprojektion. Wenn überhaupt.

|
| Fig. 9 - Projektion |
Die Erde ist ja zum Leidwesen der Kartographen keine Scheibe. Ja, ehrlich. Sie ist (fast) eine Kugel, und leider ist es unseren Wissenschaftlern noch nicht gelungen, sie einfach flach zurechnen. Alle unsere Landkarten sind daher nur Projektionen einer Kugel auf ein flaches Blatt. Sie können sich das so vorstellen, als packe man in das Zentrum eines Drahtglobus eine starke Lampe, stülpt zum Beispiel einen Zylinder mit Pauspapier darüber und kopiert die Kontinente durch.
Fertigt man eine hier dargestellte "Mercatorprojektion" an (der häufigste Kartentyp) werden horizontale Entfernungen immer breiter "aufgeschmiert", je weiter man sich vom Äquator entfernt. Um die korrekte horizontale(!) Entfernung zu ermitteln, muss man die gemessene Strecke durch den Sinus des Breitengrads dividieren um sie mit der Äquatordistanz vergleichen zu können. Aus einer Kartenstrecke die einem Kilometer pro Zentimeter am Äquator entspricht werden auf 50 Nord bereits 1.3 Kilometer! Man kann daher nicht einfach gemessene Zentimeter in Kilometer umsetzen, ohne diese Korrekturfunktion zu benutzen.
Auch auf einem Globus selbst gibt es Probleme, wenn man einfach nur die Winkelgrade zählt, die Land oder Wasser einnehmen - je näher man dem Äquator kommt, desto mehr Kilometer überdeckt ein Winkelgrad. Dies hat Smyth in seinem Buch schlicht vernachlässigt - und seit 140 Jahren schreiben Legionen von Autoren dies ab.
Nachdem ich die Widerlegung dieses Rätsels veröffentlicht hatte, traten witzigerweise Befürworter auf den Plan die das Rätsel uminterpretierten um es dennoch zutreffen zu lassen. Sie gaben ihm einen anderen Inhalt als die Rätselschöpfer vorgesehen hatten. Ohne Belege allerdings. So wurde geäußert, dass Smyth ja eigentlich den Schwerpunkt der Kontinente gemeint habe, also das Zentrum des Flächenintegrals über alle Landmassen.
Vor einigen Jahren hatte ich dies per Hand grob abgeschätzt und herausgefunden, dass der eigentliche Schwerpunkt etliche 100 km weiter östlich zu finden sein muss. Im Computerzeitalter hat glücklicherweise jemand diese Arbeit noch einmal durchgeführt. Auf Holger Isenbergs Marsverschwörer-Seiten findet man das Resultat seiner Schwerpunktberechnung[1 ]: Das Zentrum liegt ungefähr auf 35° Ost, die Pyramide auf 31° Ost. Der Meridian der den Äquator rund 450 km weiter östlich durchstößt erfüllt die Bedingung, nicht der durch Gizeh!
Allerdings akzeptierte dieser das Resultat nicht, denn nicht sein kann was nicht sein darf. Daher experimentierte er mit verschiedenen Wasserständen und fand heraus, dass die Pyramiden die Bedingung erfüllt hätten, wenn sie ein paar Dutzend Meter überflutet gewesen wären und folgerte daher, dass diese Konditionen wohl zur Zeit des Pyramidenbaus vorherrschten. Naja, die Flexibilität alternativer Geschichtsschreiber kennen wir ja inzwischen hinlänglich.
Aber wenn wir gerade so schön dabei sind, können wir en passant noch ein weiteres Rätsel "erledigen", den Landteiler.
In Rätsel (3a) schreibt Däniken: Der Meridian der durch Gizeh läuft teilt die Meere und die Kontinente in zwei gleich große Teile.
Das kann nur zutreffen, wenn auf diesem Meridian der Schwerpunkt der Landmassen liegen würde. Tut er aber nicht wie wir soeben gesehen haben, somit ist auch das Geheimnis erledigt.
Für die Rätselanhänger macht dies einen frustrierenden neuen Stand von 4:15 gegen die Dänikenschen Pyramidenrätsel.
Ein nicht in der Liste aufgeführtes Rätsel des Meisters möchte ich noch bringen, weil es gar zu kurios ist. Denn auf Seite 156 in seinem Die Augen der Sphinx schreibt er
„Ich legte eine große Weltkarte auf den Boden, nahm einen Meterstab und kniete hin. [...] Noch absonderliche Resultate erbrachte mein groteskes Spiel [naja, wenigstens sieht er es ein, Anm. FD :-)] auf dem Wohnzimmerboden, wenn ich eine Diagonale zog. Die Linie quer durch die Pyramide von Südwest nach Nordost ist die längste überhaupt mögliche Luftlinie über Landmassen rund um den Globus.“
Wie schon oben erläutert kann man Entfernungsangaben nicht ohne Korrekturen einfach auf einer Karte messen. Bei Winkeln ist dies noch viel problematischer als bei einfachen Ost-West-Entfernungen, denn hier kommen noch Winkelverzerrungen der Projektion hinein. Was EvD da als "Luftlinie" gemessen hat, ist auf einen Globus projiziert eine S-Linie! Die "echte" Streckenmessung kann man nur auf einem Globus durchführen, indem man einen "Großkreis" anlegt, der Gizeh im Winkel von 45 durchstößt. Dieser läuft rund 12000 Kilometer über Land - und dies ist mitnichten die längst mögliche Strecke über Land, denn, wie weiter oben zu lesen, läuft bereits der Breitenkreis 50 Grad Nord über 4000 Kilometer länger über Land als der 45-Großkreis durch Gizeh!
Dies ist eigentlich kein Standorträtsel, betrifft aber die Große Pyramide und ihre Umgebung. Ich habe es daher hier dazugestellt.
Das Rätsel ist erneut alt, erstmals 1902 vom englischen Esoteriker John Cotsworth in seinem Buch The rational Almanac veröffentlicht. Und wie schon so oft auf diesen Seiten gezeigt ist den heutigen Grenzwissenschaftsautoren auch hier die Originalbegründung nicht geläufig. Warum auch die Hintergründe kennen, wenn es auch so geheimnisvoll genug ist :-)
Bei Däniken klingt dieses Rätsel (9) zumindest so:
„(a) Die Pyramide ist eine riesige Sonnenuhr. Die von ihr Mitte Oktober bis Anfang März geworfene Schatten zeigen die Jahreszeiten und die Länge des Jahres an.
(b) Die Länge der Steinplatten, welche die Pyramide umgeben, entspricht der Schattenlänge von einem Tag.
(c) Durch Beobachtung dieses Schattens auf den Steinplatten konnte die Länge eines Jahres auf den 0.2419. Teil eines Tages genau angegeben werden.“
Eine Formulierung machte mich auf Anhieb stutzig: der „von Mitte Oktober bis Anfang März geworfene Schatten“. Nur viereinhalb Monate im Jahr soll diese fantastische Sonnenuhr einsetzbar sein, oder wie ist das zu verstehen? Wenn ja, ist es dann nicht eine gewaltige Verschwendung von Ressourcen, für eine derart limitierte Funktion einen solchen Riesenbau in die Landschaft zu setzen?
Aber dazu später mehr. Schauen wir uns zuerst einmal die Periode an, zu der die Pyramide zweifelsfrei als Sonnenuhr zu benutzen ist.
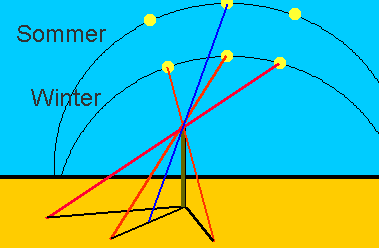
|
| Fig. 10 - Sonnenuhr |
Die primitivste Form einer Sonnenuhr ist ein Schattenstab oder Gnomon. Das ist ein senkrecht in den Boden gerammter Stab, dessen Schatten man auf dem Boden markieren kann. Dadurch dass die Sonne im Laufe des Tages über den Himmel wandert, ändert sich die Richtung des Schattens und erlaubt so die Anfertigung eines Ziffernblatts, auf dem man die Tageszeit ablesen kann.
Da die Sonne um 12 Uhr Mittags immer genau im Süden und am höchsten am Himmel steht, kann man dies geschickt als zentralen Punkt des Ziffernblatts verwenden. Klingt ja eigentlich alles ganz einfach.
Aber wie schon so oft steckt auch hier der Teufel im Detail. Im Laufe des Tages beschreibt die Sonne einen Kreisbogen am Himmel und ändert ihre Höhe am Himmel.
Aber sie beschreibt nicht jeden Tag denselben Kreisbogen. Durch die Neigung der Erdachse steht die Sonne im Sommer zur selben Zeit höher am Himmel als im Winter, wie ich schematisch auf der Zeichnung eingetragen habe. Der Unterschied im Laufe eines Jahre beträgt immerhin 47°! Das ist ein wichtiger Punkt für unsere späteren Betrachtungen.
Die Auswirkungen sind aber noch weitreichender. Durch den geänderten Sonnenlauf wandert auch die Schattenrichtung zur selben Tageszeit durch die Jahreszeiten. Unbeeinträchtigt davon bleibt lediglich der Südstand zum Mittag.
Um solche Sonnenuhren mit vertikalem Zeiger dennoch funktionieren zu lassen, kann man nicht mehr die Schattenrichtung verwenden, sondern darf lediglich die Position der Spitze auf kompliziert "korrigierten" Zifferblättern mit Konturlinien betrachten.
Die Ägypter verwendeten Sonnenuhren. Diese kamen ohne komplizierte Ziffernblätter klar, es waren sogenannte Horizzontal-Sonnenuhren, waagerechte Ost/West orientierte Balken mit einem T-förmigen Zeiger in der Mitte. Diese funktionierten prima und teilten jeden Tag in genau 12 Stunden. Leider waren diese Stunden zu unterschiedlichen Jahreszeiten unterschiedlich lang.
Ein Ausweg aus dem Dilemma wäre die Verwendung eines geneigten Zeigers in der Mitte eines halbkreisförmigen Ziffernblatts. Wenn dieser genau auf den Himmelsnordpol zeigt, kann man wieder die Schattenkante zur Ablesung verwenden. Es gibt daher auch Sonnenuhren mit dreieckigen Zeigern die einer Pyramide nicht unähnlich sehen. Aber um die Pyramide so verwenden zu können, müssten die Flanken einen Neigungswinkel von 30° anstatt der realen 52° aufweisen. Daher muss bei der Pyramide wie bei einem vertikalen Schattenstab die Spitze abgelesen werden. Eine dumme Konstruktion für hyperintelligente Weltraumaliens, wie wir gleich sehen werden.

|
| Fig. 11 - Schatten der Großen Pyramide |
Im Jahre 1997 reiste ich Ende November nach Ägypten und nahm mir am letzten Novembertag ein paar Stunden um den Mittag herum Zeit, um den Schatten zu beobachten.
Dabei konnte man schön beobachten, wie die Sonne am Vormittag immer höher stieg, und der Schatten immer kürzer wurde. Schon lange vor 12 Uhr war er zu einem schmalen Band um die Basis der Pyramide herum geschrumpft - der überhaupt keine definierte Spitze mehr aufwies.
Nicht viel besser war die Situation eine Stunde später. Das Bild oben wurde um 5 vor 1 aufgenommen. Der Spitzenbereich ist rund 5 m breit, und der Schatten selbst ist extrem verschmiert. Das Foto steilt den optischen Eindruck ein wenig auf, mein mich begleitender Arbeitskollege Stefan und ich waren 1997 nicht in der Lage, einen definitiven Schattenmittelpunkt feststellen zu können. Das liegt nicht an der heute fehlenden Spitze der Pyramide, deren Winkelauflösung wäre zu klein um einen Einfluss zu haben.
Wir hatten einige Steine ins Visier genommen und versucht zu bestimmen, wann der Stein definitiv im Schatten lag, und kamen auf eine "Ablesegenauigkeit" von knapp 10 Minuten. Für solch eine riesige Sonnenuhr eher enttäuschend.

|
| Fig. 12 - Nochmal Schatten |
Und nach ein Uhr sah die Situation noch dümmer aus. Das Bild links zeigt die Situation Ende November um 5 Minuten nach Eins: Die Spitze des Schattens ist futsch!
Wie das? Nun, die Pyramiden stehen nicht auf einer platten Ebene, sonder am Rande eines rund 40 m hohen Felskliffs zum Niltal hin. Und nach ein Uhr fällt der Schatten genau ins Tal, wo noch im 19. Jahrhundert ein Nilarm entlangfloss (es gibt wunderschöne alte romantische Fotos von Segelbooten direkt zu Füßen der Großen Pyramide - da wo das Zifferblatt gewesen sein muss :-) ).
Zu ägyptischer Zeit sah die Situation übrigens nicht anders aus, denn in antiken Zeiten befanden sich dort alte Hafenanlagen!
Ach ja, und Morgens läuft der Schatten rund 1.5 Kilometer durch die Wüste - bis zu einer Erhebung im Westen hinter der der Schatten der Pyramidenspitze verschwindet. Erst ab ungefähr 9:30 Uhr erreicht der Schatten die umgebende Nekropole und stünde für eine Ablesung zur Verfügung. Die gewaltige Sonnenuhr wäre also 4 Monate lang für je 3 1/2 Stunden am Tag nutzbar - tschuldigung, aber das ist Schwachfug.
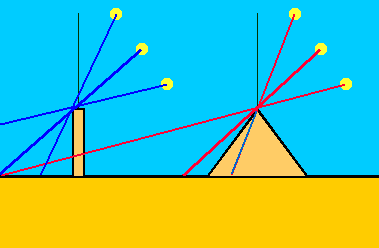
Ach ja, warum ist eine Pyramide nur für diese kurze Zeitspanne im Jahr als Schattengeber verwertbar? Das liegt an einer Eigenschaft der Form. Ein senkrechter Stab wirft immer einen Schatten, solange die Sonne nicht senkrecht über ihm steht. In Ägypten kann das nur in den südlichsten Landesteilen geschehen.
Auf der Zeichnung oben sieht man aber, wie der Schatten der Pyramide beim dritten "Sonnenstrahl" kürzer ist als die halbe Pyramidenbasis - und damit überhaupt nicht mehr sichtbar ist!
An der Großen Pyramide ist daher ab einer Sonnenhöhe von 52° kein Schatten mehr sichtbar. Um die Mittagszeit herum wird diese Höhe in Gizeh zu 2/3 des Jahres überschritten...
Die Sonnenuhrthese hat sich damit überlebt. Dennoch betrachte ich noch kurz die anderen Angaben:
Formulierung (b) und (c) sind in der Form nur Unsinn - was bitte ist die „Schattenlänge eines Tages“? Und welche umgebenden Steinplatten sind gemeint? Das Fundament ist unregelmäßig und nur noch in Bruchstücken vorhanden. Oder sind mit „Steinplatten“ die umgebenden Fürstengräber, die Mastabas gemeint?
Dänikens völlig unsinnige Beschreibung des Rätsels zeigt, dass er (wie andere Kollegen auch) überhaupt nicht an dem interessiert ist, was er da abschreibt. Der Erfinder des Rätsels, Cotsworth, stellte die Behauptung auf, dass auf der Nordseite der Pyramide ein gepflasterter Hof angelegt worden sei, der bis in eine Entfernung von 90 Metern gereicht habe. Denn dies ist die maximale Schattenlänge der Pyramide zur Mittagszeit, die bei der Wintersonnenwende erreicht wird. Der Hof sei mit regelmäßigen Steinplatten belegt gewesen, und die Schattenlänge am Mittag, zum Südstand der Sonne, sei auf diesen Platten abgelesen worden. Sie hätten Auskunft über das genaue Tagesdatum, die herannahenden Sonnenwenden, Tag- und Nachtgleichen und die Nilflut gegeben. Dies bringt nun endlich Sinn in die verworrene Däniken-Beschreibung, und es klingt auch halbwegs logisch. Nur scheitert die Idee an drei unwesentlichen Kleinigkeiten:
Inzwischen steht es beängstigenderweise 0:18 gegen die Dänikenschen Pyramidenmysterien.
Das letzte dänikensche Rätsel ist Nummer (13): „Der gesamte Flächeninhalt der vier Pyramiden-Seiten entspricht dem Quadrat der Pyramidenhöhe“
Das ist ein wenig Rechnerei, aber auch schnell erledigt. Die Pyramidenbasis beträgt 230,36 Meter, die Höhe der Pyramide 146,60 Meter. Die Höhe eines Pyramidendreiecks ist nach Pythagoras die Quadratwurzel aus (Höhe2 + halbe Grundseite2) oder 186,44 Meter. Ein Seitendreieck der Pyramide hat daher die Fläche von (186,44 m x 115,18 m) = 21474 Quadratmeter. Das mal Vier sind 85897 Quadratmeter. Die Pyramidenhöhe zum Quadrat beträgt aber nur 21491 Quadratmeter - ups! Falsch abgeschrieben, Herr v.D. :-)
Wie man sieht, entspricht der Flächeninhalt einer Pyramidenseite ungefähr dem Quadrat der Höhe - aber auch nur mit einem Fehler von 17 Quadratmetern, der Größe eines kleinen Wohnzimmers!! Viel zu ungenau um als Zeichen einer geheimnisvollen, höheren Intelligenz gedeutet werden zu können.
Endergebnis: 0:19 gegen die Zahlenmysterien!!
Das ist das Fazit aus den vorgeführten 19 Zahlengeheimnissen. Ich habe noch weitere untersucht, mit ähnlichem „Erfolg“ wie hier. Die Hauptursache für das Versagen der Thesen ist darin zu sehen, dass viele von ihnen auf veralteten Zahlen und Messungen beruhen, und sich in den letzten 140 Jahren niemand auch nur die Mühe gemacht hat, diese zu überprüfen oder neue, auf modernen Werten beruhende Rätsel zu finden. Es ist schon seltsam. Da wird der Wissenschaft Dogmatismus und das Festhalten an „antiquierten Lehrmeinungen“ vorgeworfen - und ausgerechnet die Anhänger der progressiven Ideen verbreiten seit Anno Dunnemals veraltete Behauptungen als heute noch gültige Wahrheit! Wer hängt denn da an überkommenen Lehrmeinungen fest?
Es gibt allerdings auch moderne Rätsel. Speziell seit der Entdeckung des „Marsgesichts“ in der Cydonia-Region auf dem Mars, sprossen neue Zahlenrätsel aus dem Boden, die die Pyramiden mit dem Sonnensystem in Verbindung bringen wollen. Mit kompliziertesten Berechnungen werden Karten des Sonnensystems in die Pyramiden projiziert, und sogar Karten des Gizeh-Plateaus über Bilder aus Sci-Fi-Filmen gelegt um kosmische Zusammenhänge zwischen Gizeh, Arthur C. Clarke und Stanley Kubrick zu finden. Eine der jüngeren „Entdeckungen“ beweist leider, dass auch diese modernen Pyramidenmystiker eines immer noch nicht beherrschen: Das Nachprüfen ihrer Quellen. So beglückte Holger Isenberg die Netzgemeinde mit folgender Erkenntnis (Tabelle von mir formatiert):
"Unglaublich!
Die Massenverhältnisse der Pyramiden stimmen nahezu exakt mit denen der 3 potentiell bewohnbaren Planeten im Sonnensystem überein!
Hat jemand eventuell exaktere Masse der Pyramiden? Ich fand auf die schnelle nur diese mit unbekannter Quelle:
Pyramide Volumen Größe % Khufu 481x775.75^2/3=96486686 f3 100% Khafra 471x707.75^2/3=78642880 f3 82% Menkaure 218x356.5^2/3=9235370 f3 10%
Planet Masse Masse % Erde 5.9736 x 1024 kg 100% Venus 4.869 x 1024 kg 82% Mars 6.4219 x 1023 kg 11%
Quelle:
Brian Crowley, Anthony Pollock: "Return To Mars"
Ursprünglich aber von Willy Kross.
Soweit Holger Isenberg. Während die Planetenmaße noch halbwegs stimmen, liegen die zur Erzeugung des Rätsels verwendeten Pyramidenmaße ganz schön daneben. Das Verhältnis der Planetenmassen beträgt[2 ]:
| MErde | 100 % |
| MVenus | 81,4 % |
| MMars | 10,7 % |
Die Pyramidenmaße[3 ]:
| Pyramide | Breite | Höhe | Volumen | % |
|---|---|---|---|---|
| Cheops | 230,36 m | 146,5 m | 2,591 Mio m3 | 100 % |
| Chephren | 215,25 m | 143,5 m | 2,216 Mio m3 | 85 % |
| Mykerinos | 104,60 m | 66,54 m | 0,242 Mio m3 | 9 % |
Prozentual sehen die Fehler minimal aus, rechnet man aber die Abweichungen von 3.6% bzw. 1.7% in Kubikmetern aus, erhält man Bauabweichungen von schlappen 93000 m3 bei der Chefrenpyramide und 44100 m3 bei der Mykerinos - Pyramide. Das entspricht Würfeln von 45 bzw. 35 m Kantenlänge. Im Vergleich zum Volumen der jeweiligen Pyramide muten die Fehler noch grotesker an, die 44100 m3 Baufehler der Mykerinospyramide entsprechen immerhin rund 20% des Volumens dieser Pyramide!!! Von bewusster Ähnlichkeit kann bei solch gigantischen Abweichungen keine Rede mehr sein. Sollten dies also wirklich Aliens „verbrochen“ haben, müssen diese ganz schön dumm gewesen sein :-)
Die Erklärung/Entschuldigung ließ nicht lange auf sich warten: Seien auch die Pyramidenmäntel berücksichtigt worden? Ja, sind sie :-) Und außerdem solle man genauere Daten verwenden, bei denen auch Hohlräume und die spezifischen Baumaterialien berücksichtigt seien. Nun, Hohlräume hat nur die Cheopspyramide, rund 1200 Kubikmeter oder 0.4% des Pyramidenvolumens. Da gibt's nix zu korrigieren. Und alle drei Bauten bestehen aus demselben Material, das sogar aus denselben Steinbrüchen stammt. Wie man es dreht und wendet: Ein neuer Schuss in den Ofen.
Hans Jelitto, seines Zeichens Physiker und Mathematiker, Scientologe und beteiligt an der Planung des Mystery-Parks von Däniken, brachte vor einigen Jahren das Buch „Pyramiden und Planeten“ heraus, in dem auch er gar lustige Zusammenhänge zwischen den Pyramiden und Körpern unseres Sonnensystems herstellen wollte. Zu Zeiten des alten A.A.S.-Forums beschäftigte ich mich ein wenig damit, stellte aber schnell fest, dass er nicht anders vorging als seine numerologischen Brüder. Daher wollte ich mich eigentlich nicht weiter mit ihm beschäftigen.
Im Februar 2007 kontaktierte mich ein Leser seines Buchs und sprach mich auf eine These daraus an, die auf den ersten Blick wegen ihrer Genauigkeit überzeugend wirkt. Denn es soll die mittlere Pyramidengrundkante geteilt durch eine Lichtsekunde genau dem Erdvolumen geteilt durch das Sonnenvolumen entsprechen! Na, das wär ja was.
Jelitto verwendete allerdings offenbar eine falsche Kantenlänge von 230,263 cm, anstatt der korrekten 230,36 cm[4 ]. Aber lassen wir das erst mal.
Der aktuelle Wert für Erdvolumen/Sonnevolumen ist 0,00000076711, die Kantenlänge der Pyramide durch die Vakuumlichtgeschwindigkeit mit Jelittos Wert 0,00000076805, mit dem Korrekten Wert 0,00000076818. In der Tat, die Fehler sind sooo minimal, dass man von einer Übereinstimmung ausgehen muss.
Wirklich? Nein, denn Jelitto benutzt einen ganz einfachen Trick. Ein winziger Wert, geteilt durch einen riesigen Wert, gibt eine sehr kleine Zahl mit minimalst wirkenden Abweichungen. Eigentlich eine völlig sinnlose Darstellung. Interessant ist der Kehrwert: Wie oft passt die Erde in die Sonne, und die Pyramidengrundseite in die Lichtsekunde!
Schauen wir uns mal das Ergebnis an: In ein Sonnenvolumen passen 1.303.600 Erdvolumen hinein, in eine Lichtsekunde allerdings 1.301.999 bzw. 1.301.773 Pyramidenkantenlängen. Die Differenz beträgt 1601 (Jelittos Basisbreite) bis 1827 Erdvolumen! Das ist kein Rundungsfehler mehr.
Man kann übrigens auch berechnen, wie breit die Pyramide denn sein müsste, um das Rätsel zu erfüllen. Man staune: 228,22 Meter, das liegt nahe an den Schätzungen, die Smyth damals für seine allerersten Spielchen verwendete.
Aber - nein, Jelitto wird doch nicht??? Oder doch...
| Anmerkungen: | ||
| [1 ] | Der Autor wollte eigentlich genau das Gegenteil beweisen, nämlich dass die Behauptung korrekt ist. Immerhin ist er so fair, auch das negative Resultat zu veröffentlichen. | |
| [2 ] | K.R.Lang/C.A. Whitney; Planeten, Springer 1991, S. 370 | |
| [3 ] |
Verner, Die Pyramiden Dorner; Die Absteckung und astronomische Orientierung ägyptischer Pyramiden; S. 506, 507: | |
| [4 ] | gefolgert aus einer vorherigen Rechnung, bei der er mit einer falschen Pyramidenhöhe den π-Wert bestimmte | |