

Kommen wir zum nächsten Problem: wWe kommen die Steine rauf auf die Pyramiden? Die meisten Ägyptologen favorisieren den Pyramidenbau mit Hilfe von Rampen, obwohl viele von ihnen, wie ich in privaten Korrespondenzen erfuhr, nicht genau verstehen warum. Auch interessierten Laien ist zum Beispiel oft nicht klar, warum das Ziehen von 100 Kilogramm eine schräge Rampe hoch einfacher als das senkrechte Anheben dieser Last ist.
|
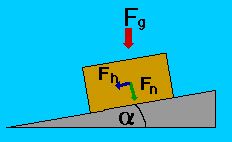
| Fig. 1 – Schiefe Ebene |
Auf der letzten Seite habe ich ja das Transportprinzip auf einer ebenen Unterlage besprochen. Ein Ein-Kilo-Gewicht drückt dabei mit einer Kraft von 10 Newton auf die Unterlage, um es nach oben zu bewegen (mit zu vernachlässigender Beschleunigung) braucht man auch 10 Newton. Stellen wir das Gewicht nun auf eine geneigte („schiefe“) Ebene, passieren seltsame Dinge.
Das Gewicht fängt an, die Rampe herunterzurutschen. Aber wie viel Kraft braucht man, um es daran zu hindern, es also oben zu halten? „Na, auch Deine 10 Newton“ bekam ich überwiegend zu hören. Aber das ist falsch, es ist viel, viel weniger, und das ist das Geheimnis der Rampe..
Die Kraft, die das Gewicht die Rampe entlang nach unten zieht nennt man Hangabtrieb. Sie ist abhängig vom Neigungswinkel α. Bei α = 0° ist diese Kraft logischerweise Null, es gibt ja nichts zum Hinrutschen, und bei α = 90°, also an einer senkrechten Wand, ist der Hangabtrieb gleich der Gewichtskraft. Bei allen anderen Neigungen liegt sie darunter.
Sie ist proportional zum Sinus des Neigungswinkels, die Formel: Fh = Fg * Sinus(α).
Der Sinus ist eine so genannte trigonometrische Funktion, denn das Verhältnis zwischen Neigung und Kraft ist nicht linear. Es nimmt bei flachen Rampen schneller, und bei steileren Rampen langsamer zu, wenn man die Steigung erhöht. Ein Beispiel:
Ein Kilogramm hat bei 5° Steigung einen Hangabtrieb von 0,87 N, und bei 6° einen von 1,05 N. Der Unterschied beträgt also 0,17 N.
Auf einer 45° steilen Rampe hat unser Kilo einen Hangabtrieb von 7,07 N, bei 46° einen von 7,19 N, die Differenz beträgt nur noch 0,12 N.
Auf einer 5° steilen Rampe, die ich von nun an betrachte, „wiegt“ ein Kilo also nur noch 87 Gramm? Antischwerkraft? Was ist mit den anderen 913 Gramm geschehen? Nein, verschwunden sind die nicht. Die schiefe Ebene spaltet die Gewichtskraft in zwei Komponenten auf, den schon betrachteten Hangabtrieb, und in die sogenannte Normalkraft, die senkrecht zur Rampenoberfläche steht, und das Gewicht dagegen presst. Eben mit den „verschwundenen“ 913 Gramm bzw. 9,13 Newton. Beide Kräfte zusammen entsprechen wieder vom Betrag her der Gewichtskraft.
Auf der vorherigen Seite habe ich ja schon das Konzept der Reibung vorgestellt. Diese Kraft ist abhängig vom Reibungskoeffizienten und der Gewichtskraft. Auf einer platten Ebene. Auf einer Schräge ist sie nicht abhängig von der Gewichtskraft, sondern von der Normalkraft. Diese ist auf einer horizontalen Fläche identisch mit der Gewichtskraft, und an einer senkrechten Fläche Null. Sie verläuft genau invers zum Hangabtrieb, nämlich mit dem Cosinus des Neigungswinkels α.
Ich betrachte hier nur die so genannte Gleitreibung, um die Sache nicht unnötig zu verkomplizieren.
Bei 5° Steigung beträgt die Normalkraft unseres Kilos 9,96N, bei 6° 9,94 – eine Differenz von gerade einmal 0,017 N.
Bei 45° bekommen wir eine Normalkraft von 7,07 N, bei 46° eine von 6,95 N – eine Differenz die mit 0,125 N über sieben mal größer ist.
Bei 5° beträgt die Reibungskraft mit dem auf der vorherigen Seite besprochenen Reibungskoeffizienten von 0,25 also 2,49 N.
Mit welchem Winkel soll man also Rampen bauen? Die Zugkraft, um eine Last eine Rampe hoch zu schleppen, besteht offenbar aus der Summe zweier Teilkräfte, nämlich dem Hangabtrieb und der Reibungskraft.
In der folgenden Tabelle habe ich einmal exemplarisch die Zugkraft Fz = Fg * sin(α) + μ * Fg * cos(α) für einige Materialkombinationen (und somit Reibungskoeffizienten) für unser Kilogramm zusammengestellt.
Die eine Kraft nimmt mit höherer Steigung zu (Hangabtrieb), die andere nimmt ab (Reibung). Gibt es da vielleicht eine optimale Neigung?
Als Materialkombination bevorzuge ich die Kombination von Holz (für den Transportschlitten) auf Schotter, dort habe ich in Experimenten je nach mittlerer Korngröße ein μ zwischen 0,18 und 0,30 ermittelt, für meine Berechnungen auf den Folgeseiten verwende ich einen Mittelwert von 0,25.
| Material | μ | Ebene | 5° | 10° | 15° | 20° | 25° | 30° |
|---|---|---|---|---|---|---|---|---|
| Holz/Schotter min | 0,18 | 1,80 N | 2,66 N | 3,51 N | 4,33 N | 5,11 N | 5,86 N | 6,56 N |
| Holz/Schotter med | 0,25 | 2,50 N | 3,35 N | 4,20 N | 5,00 N | 5,77 N | 6,50 N | 7,17 N |
| Holz/Schotter max | 0,30 | 3,00 N | 3,86 N | 4,69N | 5,49 N | 6,24 N | 6,95 N | 7,59 N |
| Holz (Eiche)/Holz trocken | 0,34 | 3,40 N | 4,26 N | 5,09 N | 5,87 N | 6,61 N | 7,30 N | 7,94 N |
| Holz (Eiche)/Holz nass | 0,25 | 2,50 N | 3,35 N | 4,20 N | 5,00 N | 5,77 N | 6,50 N | 7,17 N |
| Stahl/Stahl | 0,12 | 1,20 N | 2,07 N | 2,92 N | 3,75 N | 4,55 N | 5,31 N | 6,04 N |
| Gummi/Asphalt | 0,85 | 8,50 N | 9,33 N | 10,1 N | 10,8 N | 11,4 N | 11,9 N | 12,4 N |
Offensichtlich leider nein. Die aufzuwendende Zugkraft steigt und steigt und steigt, sodass man sinnvollerweise mit der kleinsten Steigung von 5° arbeitet.
Die Ägypter maßen nicht in °, sie verwendeten Böschungsverhältnisse und verwendeten wahrscheinlich zwischen 2 und 3 Fingern zur Elle, das wären zwichen 4° und 6° gewesen, passt also.
|
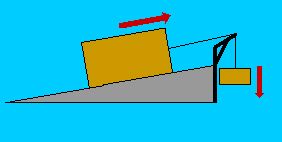
| Fig. 2 – Perpetuum Mobile? |
"Moment mal", werden sich jetzt einige schlaue Köpfe denken. "Wenn die Transportkraft eines Steins eine Rampe hoch nur 1/3 der Gewichtskraft beträgt, kann ich doch 3 Steine nach oben ziehen, indem ich einen Stein nach unten abseile!". Die Erfindung des Perpetuum Mobile? Das Ende aller Energieprobleme?
Leider nein. Die angenommene 5°-Rampe ist bei einem Meter Höhenunterschied immerhin 12 Meter lang! Um einen 2500-kg-Block über die Rampe nach oben zu ziehen, müsste ein 840-kg-Stein als Gegengewicht insgesamt 12 mal um einen Meter angehoben und wieder heruntergelassen werden! Selbst in einer reibungslosen Welt müsste ein 217-kg-Stein als Gegengewicht 12 mal nach oben befördert werden. Und für beide Vorgänge benötigt man dieselbe Arbeit!
Arbeit ist auch ein physikalischer, messbarer Begriff, nämlich "Kraft mal Weg". Sie wird in der physikalischen Einheit "Joule" gemessen. In der reibungsfreien Welt müssen 2170 N über einen Weg von 12 Metern aufgebracht werden - das sind 26040 J. Hebe ich 12 mal das Gegengewicht von 217 kg an, ist das Ergebnis wiederum 26040 J! Die Physik schenkt einem nichts!
In der realen Welt ist es durch die Reibung noch übler. Benötigt ein 2.5 Tonnen-Block eine Arbeit von 25000 J um ihn um einen Meter zu heben, wird auf der Rampe glatt das Vierfache verpulvert!
Lohnt sich denn das? Ja. Wir Menschen sind in der Lage, erhebliche Arbeit zu verrichten, aber unsere Kräfte sind beschränkt. Daher zielen alle einfachen Maschinen wie Hebel und Flaschenzüge darauf ab, den Krafteinsatz zu reduzieren, selbst wenn dadurch der Arbeitseinsatz vergrößert wird.
Jetzt haben wir alles zusammen um zu kalkulieren, wie viele Arbeiter man denn nun wirklich braucht, um einen typischen Pyramidenblock über eine Rampe auf die Pyramide zu schleppen.
Ein heutiger Transport- oder Lagerarbeiter kann durchaus 50 Kilogramm-Säcke tragen. Über kurze Strecken und für kurze Zeit. Über einen 8-Stundentag in sengender Hitze ist wohl nicht anzunehmen. Ein 50 kg-Sack übt eine Gewichtskraft von 500 N auf.
Interessanterweise konnte ich in Experimenten problemlos mit 500 N ziehen, ich schleppte dazu ein entsprechendes Gewicht einen Schotterplatz entlang. Das können Sie auch mal ausprobieren, zum Beispiel in einem Sportstudio.
Der Grund für diesen Unterschied: Beim Ziehen kann man durch Vorüberneigen sein eigenes Körpergewicht als Kraftquelle verwenden. Beim Tragen hingegen muss das Körpergewicht zusätzlich zur Last unterstützt werden. Beim Ziehen kommt die meiste Kraft aus den kräftigen Beinen. Beim Heben geschieht dies oft mit den wesentlich schwächeren Armen.
All dies führt dazu, dass beim Ziehen dauerhaft eine Kraft von bis zu 1000 N aufgebracht werden kann. Gehe ich von 500 N aus, um auf der sicheren Seite zu bleiben, kann ein 2.5-Tonnen-Stein auf einer 5°-Schotterrampe mit (8400 N / 500 N) = 16.8 Arbeitern gezogen werden!
Wie viele der von selbst von von Däniken zugegebenen Seilen benötigt man dazu? Bei einer Reißfestigkeit von gemittelten 60 N/mm2 einen Gesamt-Seilquerschnitt von 140 Quadratmillimetern. Das entspricht einem Seildurchmesser von 1,34 Zentimetern! Selbst die schwersten Blöcke von 50-70 Tonnen Gewicht kämen mit 2800-3920 Quadratmillimetern Seilquerschnitt aus. Das entspräche einem Seil von 5,9 bis 7,1 cm Durchmesser - oder 20-28 Seilen der bekannten Dicke von 1,34 Zentimetern! Das ist nichts was auch nur annähernd in den Bereich des Unwahrscheinlichen oder gar des Unmöglichen fällt.
Mit diesem Basiswissen versehen, können wir uns einige Gedanken zum Rampentransport von Steinen ansehen.