

|
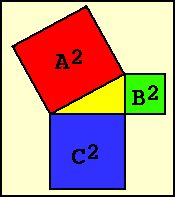
| Fig. 1 – Theorem of Pythagoras |
The theorem of Pythagoras is the second largest numerological pyramid mystery in and around Giza. I don't know if pi or Pythagoras is the most published one, but to the later some modern papers have been published. One of them will be discussed on the next page.
Like pi, the theorem of Pythagoras is no rocket science although the picture looks complicated enough for the laimen.
Pythagoras, a Greek philosopher and mathematician (c. 570-480 BC), fas founder of a philosophical school which claimed, that music and numbers were the basis of this world. Therefore the Pythagoreans looked for mathematical laws nature was supposedly based on.
The most famous laws they discovered deals with right-angled triangles. These are triangles where two sides form a right angle, one with 90°. The two sides forming this angle are called cathetes, the side connecting the two cathetes is called Hypotenuse. The Pythagoreans found out:
The mathematical description of the picture on the side is therefore : A2 = B2 + C2 . And this should be somewhere in Giza. Let's have a look.
Erich von Däniken claims in riddle (6): "The three pyramids of Giza are arranged in a pythagoreic triangle, the sides are in a 3:4:5 ratio.". This claim is very doubtful...
|
| Fig. 2 – Giza triangle |
To see that there is no right angled triangle anywhere around only a look on a map of the pyramids is necessary (if you know what a right angled triangle is, of course :-) ). All three pyramids are standing nearly on a line (in the Orion Mystery I will take a closer look at the “Giza-diagonal”), only the centre of Menkaure's pyramid deviates a little bit to the east of this line. Surely, there is no squared triangle in sight, even more no 3:4:5-triangle. The claim of von Däniken is pure rubbish and a gain a sign, that he doesn't know what he writes about, or that he doesn't care.
The "ratio of 3:4:5" is also mentioned in books from authors knowing more about it. The already mentioned Piazzi Smyth wrote about it in 1864. But he did not mean the arrangement of the pyramids, as von Däniken claims, but the length of the pyramid sides
The length of the three large Giza pyramids (Khufu, Kafre, Menkaure) should have a 3:4:4 ratio. If this is the case there must be a common measurement unit which is three times in the base length of Menkaure's pyramid, four times in that of Kafre and 5 times in that of Khufu.
This can also be checked quickly with a pocket calculator Let us look first for a common base unit:
| Pyramid | Base length | Factor | Length/Factor |
|---|---|---|---|
| Khufu | 230,36 m | 5 | 46,07 m |
| Kafre | 215,50 m | 4 | 53,87 m |
| Menkaure | 108,50 m | 3 | 36,16 m |
Hm, not very convincing. The “common base unit” has a range between 36 and 53 meters – a difference of 67%. We can see how big the pyramids must be to be built in one of the uncommon base units:
| Base unit | Khufu | Error | Kafre | Error | Menkaure | Error |
|---|---|---|---|---|---|---|
| Khufu | 230,36 | 0 m | 184,28 m | -31,22 m | 138,21 m | +29,71 m |
| Kafre | 269,35 m | +38,99 m | 215,50 m | 0 m | 161,61 m | 53,11 m |
| Menkaure | 180,80 m | 49,56 m | 144,64 m | -70,86 m | 108,50 m | 0 m |
No, so common base unit, and the pyramids have definitively no 3:4:5-ratio
To the excuse of Smyth we must say, that to his time the pyramid bases were covered in meter high heaps of rubble, and that he used only estimations as basis for his calculations. Estimates he made to fit his theories, of course. Since Petrie published his “Pyramids and Temples of Giza” in 1883 these “mysteries” should have vanished – well, probably not...
There is another interpretation found on web sites and in books. Therefore the areas of the base squares of the pyramids have a 3:4:5-ratio This too can be checked (and disproved) in a few seconds. Khufu's pyramid covers an area of 53075 square meters, Kafre's 46440 square meters and the one of Menkaure 11772 square meters. The added areas of Kafre and Menkaure cover 58212 square meters, 5137 more than the pyramid of Khufu. This is not a small error, it equals the area of a pyramid with a base length of 71 meters. No, this claim again is wrong.
After this new fiasco for Erich von Däniken and other numerologists, 10 riddles have been disproved, only 9 are left!
By the way, there IS a 3:4:5-triangle at Giza. But nowhere the numerologists search for it. It is built into Kafre's pyramid. This triangle, called “holy triangle” by some authors, should also be a sign of Atlanteans or small furry animals. Why?
Normally, the sides of a right angled triangle have no whole unit fractions since they are square roots. If you measure one cathete to 4 units and the other one to 6 units, the hypotenuse would be sqrt(4*4 + 6*6) = 6.92 units long. The Egyptians had no knowledge of square roots, but they needed right angled triangles to measure land after each Nile flood and to calculate the taxes. Fortunately, there are a few triangles where all three sides have whole unit lengths, the smallest one has sides of 3, 4 and 5 units (32 + 42 = 25 = 52)!
But what do you need those triangles for? Well, to measure new fields without ever measuring an angle. If one takes a rope with (3+4+5) knots, fastens the first knot where you want to start measuring, then goes three knots in the direction of the base side you want to measure, fix the knot there too, go in the assumed direction of the side line of the future field for four knots, hold this knot there and send one with the rest of the rope to the first knot, you automatically get a right angle between the sides with 3 and 4 knots when the 4th knot man pulls the 5 and 4 knot-sides tight. It can be fixed there too, and by releasing the third knot and pulling it to the other side, you get a perfect rectangle with the side lengths of 3 by 4 units. Without ever measuring an angle. Several pyramid chambers were obviously constructed with this method, too.
But to construct such a triangle, you need knowledge about the theorem of Pythagoras AND about square roots. Still a sign of ancient astronauts or small furry animals?
Not necessarily. As I found out in an experiment, these ratios can be found very easily without knowing the theorem. You only need a long rope with many equidistant knots, three helpers and a right angle. You work like above. Fix knot one, go along the base line the wished number of knots, fix the second knot, measure the right angle, go the wished number of knot, fix this too and go with the rest of the rope back to knot one.
After a while you find out, that with some knot ratios of the first two sides you get a not of the loose end exactly together with the first fixed one – and that you do not need to know to measure the right angle at all. For this one needs no God or ancient astronauts – or small furry animals from α Centauri.
|
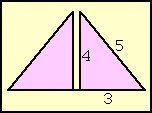
| Fig. 3 – Pyramid section |
Well, there is a small difference between measuring a field and putting a holy triangle into the second largest building of antiquity. Sawing the pyramid of Kafre into two halves (children, please don't do that at home) we see, that each quarter section has an exact 3:4:5-ratio. The proof of higher knowledge!
I know that you don't want to hear it (boooooring), but it isn't. The Egyptians had indeed no chance NOT to include this triangle – not in the pyramids built with a 21:1 slope. You remember? Pi-ramid? Slopes? Finger-cubit-ratios? Kafre's pyramid was built with a run of 21 fingers to the rise of 28 fingers (one cubit). So we have 21:28 fingers. We can divide this by 7, and get a 3:4-ratio – two sides of a 3:4:5-triangle. In all 21:1 pyramids. Without any knowledge about higher mathematics or geometry.